↓Skip to main content
  1. Posts/

SPECHT.jl: Adaptive contrastive learning for unbiased object detection in superresolution microscopy

··1273 words·6 mins
Table of Contents

Problem statement #

How do you detect objects in superresolution microscopy when:

  • signal to noise ratio varies a lot
  • you need stable detection across channels
  • unbiased with respect to small or large objects
  • you only have weak supervision

In this post I’ll describe the idea behind using fuzzy computing and belief theory to achieve all of the above. Code and paper are available online.

Note, images are sourced from this paper, to which I hold author copyright.

In a nutshell, this image shows what we’re trying to do. Given two series of images with contrasting labels X and Y, detect objects that are unique or common to either/both. For example, imagine the label X=healthy, and Y=infected.

Contrastive learning

Adaptive object detection #

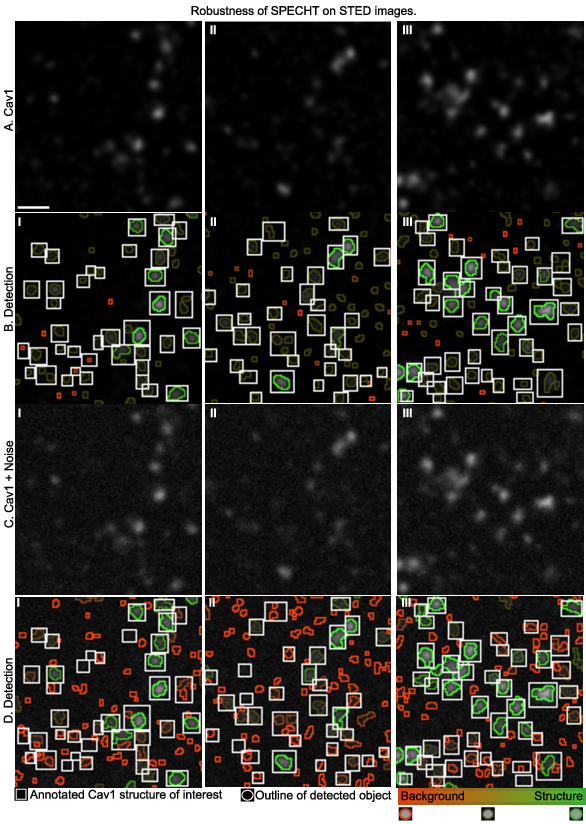
In superresolution imaging you do not have the same rich texture as you do in natural images (cats and dogs), and factors such as variation in noise and labelling (fluorescence intensity) can vary a lot. It’s therefore critical to detect objects fairly, with recall and precision high for both small and large objects.

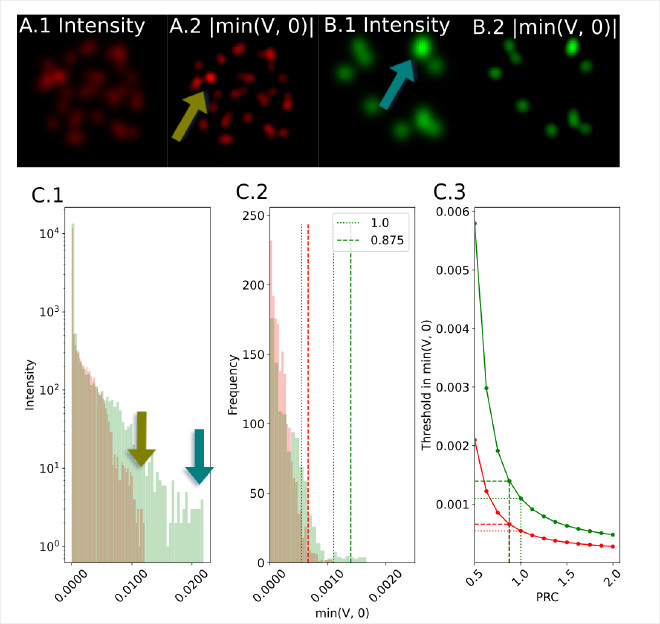
Using Kurtosis scaling for detection
To ensure accurate detection we use the 2nd differential of intensity, then look at the distribution of its long tail. In the above image you can see that a shift in faint versus bright objects induces such a shift, therefore the detection needs to compensate for it to remain unbiased. Let V be the 2nd differential of the intensity of the image, we then normalize: $$ Z(V) = \frac{V - \mathbb{E}[V]} {\sigma V} $$

We want to use Z(V), the z-score of the differential to scale with the distribution, as a threshold. However, Z can be unstable due to long tail effects. Instead, the kurtosis, or 4th moment, captures the tail of the distribution. We prove that the kurtosis of the image intensity (I) is a lower bound to the expected value of the differential: $$ \sqrt[4]{k(I)} \leq \mathbb{E}[Z(V)] $$ We can scale this factor by a linear weight, panel C shows how this behaves consistently for markedly different images.

Learning which objects are unique #

We use belief theory, a superset of probability theory, to detect which objects are unique to a weak label.

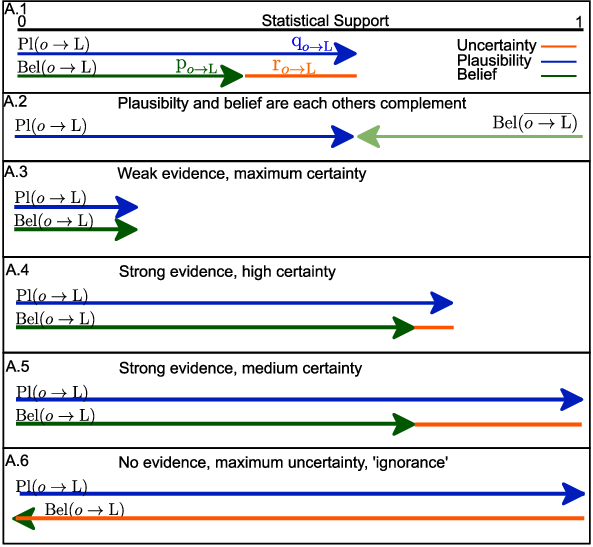
belief
For each object, we can learn the minimum and maximum evidence each object has a for a label. Contrasting these then allows us to learn succinct representations that we can leverage across many labels. In contrast, this is hard to do with techniques such as MIL where nested labels are non-trivial to support. In order to leverage belief theory, we prove using Cantelli’s theorem that we can find a minimal evidence (belief) for each object. Let Lj be a label, \(L_j, x_k, \mu_J, \Sigma_J\) be the j’th label, feature descriptor of the k’th object, and mean/sd of the label J’s feature distribution, we can compute the Mahalanobis distance for each object k to the label J: $$ D_j[k] = \sqrt{(\vec{x_k}-\vec{\mu_J})^T \Sigma_J^{-1}(\vec{x_k}-\vec{\mu_J})} $$ We then normalize this: $$ Z_j \gets \frac{D_j .- \mathbb{E}[D_j]}{\sqrt{\mathrm{Var}(D_j)}}. $$

so we can use Cantelli’s theorem to prove an upper bound (plausibility) that the k’th object is representative to label J: $$ \text{Pl}[o_k \rightarrow L_J] \gets \frac{1}{1+Z_j[k]^2}. $$ Once you have a plausibility function for each label, you can compute the other complementary functions and use the axiomatic framework to compute more complex expression. See my previous posts (I, II, III) for more in depth coverage.

Learning to detect protein structures by weak label alone #

We can now apply our model to a real world use case, the detection of caveolae in 2D STED superresolution microscopy. Caveolae are structures formed from Cav1 protein building blocks, and are critical to offer cells a buffer against chemical and physical stressors. Quantifying how many are (intact) in the cell membrane allows for example testing if certain drugs affect metastasis of cancer cells.

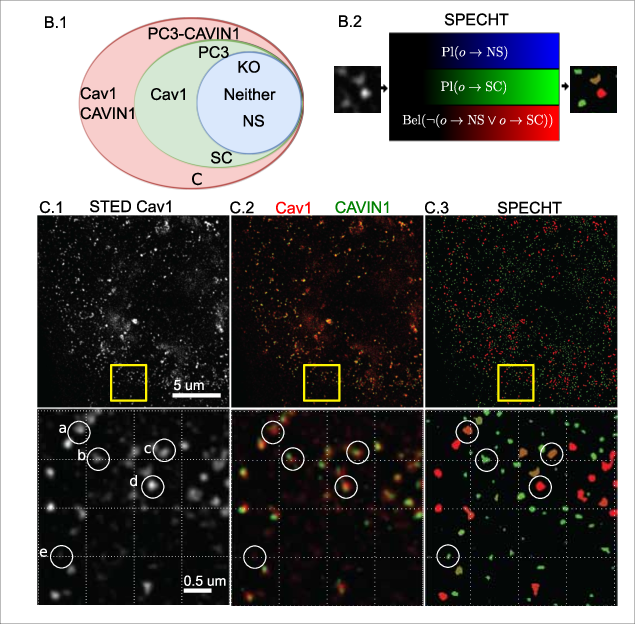
Caveolae

Noise as an implicit label #

Noise, or non-biological fluorescent signal, can also be modelled by the object labelling stage. Instead of trying to denoise or filtering out the noise, which requires understanding of the complex noise model of SRM microscopes, we can instead let the model learn what is noise by giving it background only images, and then let it label the actual noisy labelling in real images. If the noise then is increase,d we see in the below image that the detection accurately picks up the noisy objects as non-biological (red).

Noise

Fuzzy computing gives us a way to express disagreement between models #

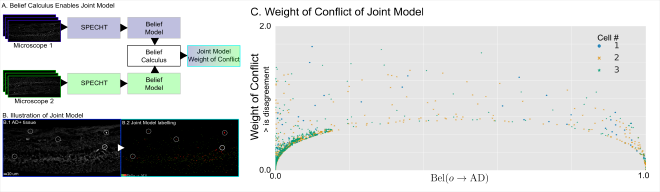
Belief theory allows us to define how two models conflict or agree, at a per object level. This is illustrated in this figure, where SPECHT is trained on 2 different sets of images. Such a scenario occurs for example between acquisitions, or operators, or hospitals. Rather than using different models, we can compute the joint belief of the model.

Conflict

Future work #

In future work I will explore the effect of the novel concept of pignistic belief functions, which leverage an attention based mechanism at a mathematical level, that avoids a lot of the issues that the severaly imbalanced data in biomedical image analysis induces.

Publication #

SPECHT was published in the following works:

  • Ben Cardoen, Timothy H. Wong, Parsa Alan, Sieun Lee, Joanne Aiko Matsubara, Ivan Robert Nabi, and Ghassan Hamarneh. SPECHT: Self-tuning Plausibility Based Object Detection Enables Quantification of Conflict in Heterogeneous Multi-scale Microscopy (Nabi and Hamarneh: Joint senior authors). PLOS ONE, 17(12):e0276726, dx.doi.org/10.1371/journal.pone.0276726 2022.

  • Parsa Alan, Bharat Joshi, Ben Cardoen, Kurt Vandevoorde, Guang Gao, Peter Overby, James D. Johnson, Ghassan Hamarneh, and Ivan Robert Nabi. Basal Gp78-dependent mitophagy promotes mitochondrial health and limits mitochondrial ROS (Alan, Joshi, Cardoen, and Vandevoorde: Joint first authors; Hamarneh and Nabi: Joint senior authors). Cellular and Molecular Life Sciences (CMLS), 79(565):1-20, 2022. 10.1007/s00018-022-04585-8, 2023.

  • Parsa Alan, Bharat Joshi, Ben Cardoen, Kurt Vandevoorde, Guang Gao, Peter Overby, James D. Johnson, Ghassan Hamarneh, and Ivan Robert Nabi. Basal Gp78-dependent mitophagy promotes mitochondrial health and limits mitochondrial ROS (Alan, Joshi, Cardoen, and Vandevoorde: Joint first authors; Hamarneh and Nabi: Joint senior authors). In American Society of Cell Biology (ASCB) - Cell Bio, 2022.

  • Parsa Alan, Kurt Vandevoorde, Bharat Joshi, Ben Cardoen, Guang Goa, Ghassan Hamarneh, and Ivan Robert Nabi. Basal Gp78-dependent mitophagy promotes mitochondrial health and limits mitochondrial ROS. In UBC SBME 2022, 2022.

  • Ben Cardoen and Ghassan Hamarneh. Learning to look beyond what we can see: Leveraging statistical learning to improve scientific discovery from fluorescence microscopy. In Biomedical Imaging and Artificial Intelligence (BMIAI) cluster Fall Research Showcase, Vancouver, Canada, pages 1, 2021.

  • Ben Cardoen, Timothy H. Wong, Parsa Alan, Sieun Lee, Joanne Aiko Matsubara, Ivan Robert Nabi, and Ghassan Hamarneh. Self-tuning Weakly Supervised Object Detection (SPECHT) of Sub-Diffraction Limited Caveolae and Scaffold and Amyloid-Beta Deposits. In American Society of Cell Biology – Cell Bio 2021, 2021.

  • Ben Cardoen, Timothy H. Wong, Ivan Robert Nabi, and Ghassan Hamarneh. Belief theory enables detection of Caveolae in superresolution microscopy. In Microscopy Societies Symposium - Advanced Imaging and Analysis at Nanoscale, November 2021.

  • Ben Cardoen, Timothy H. Wong, Parsa Alan, Sieun Lee, Joanne Aiko Matsubara, Ivan Robert Nabi, and Ghassan Hamarneh. Automatic identification of protein complexes in multi-scale microscopy with applications tometastasis and Alzheimer disease. In The 2nd Annual Tri-Cluster Research Day, Canada, pages 1, 2020.

  • Ben Cardoen, Timothy H. Wong, Parsa Alan, Sieun Lee, Joanne Aiko Matsubara, Ivan Robert Nabi, and Ghassan Hamarneh. Belief theory enables identification of protein complexes in multi-scale microscopy with applications to metastasis and Alzheimer disease. In Centre for Artificial Intelligence Decision-making and Action (CAIDA), BC’s AI Showcase, Canada, pages 1, 2020.

↑