ERGO: Unbiased prediction of imbalanced localizations in superresolution microscopy using graph tiling heuristics and temporal learning

Problem statement #

Interaction in SMLM (dSTORM specifically) depends on accurate reconstruction (localization) across multipe channels. High density of emissions can paradoxically compromise localization. Here we use an LSTM neural network, combined with a graph tiling heuristic to predict localization density, improving markedly on the state of the art. Code and paper are available online, images are adapted from the preprint version.

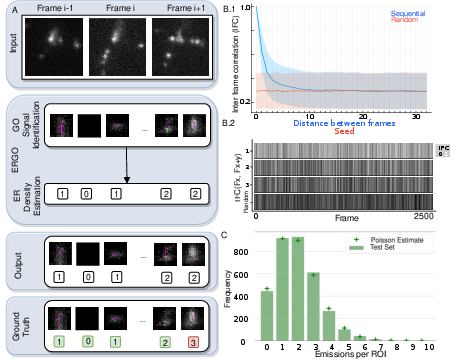
The problem is illustrated in the below image, high density can cause artifacts with a severe error in localization.

An SMLM localization algorithm sees fluorescence emissions (‘blinks’) and tries to produce 3D localizations. The input is a stream of frames with potential emissions. First, we need to divide and conquer, by splitting up the image into ROIs, and passing those to the density prediction algorithm.

Looking at the distribution of the density shows that it’s clearly Poisson distributed with \(\lambda\) of +- 1.8. We can also see that the temporal correlation of emissions spans about 4 frames, which we can use.

Method #

Because localizations are temporally correlated, we can use an LSTM to learn the emission density. But first we need to decouple the network from the raw input to mitigate some of the extreme imbalance, and to maximize spatial correlation. We’ll split the frame into ROIs use a graph tiling heuristic, and then feed in those ROIs to the LSTM.

Graph tiling heuristic #

First we select local intensity maxima (red), who are connected in a minimum spanning tree with maximum distance d. An ROI is placed on the centroid of each subgraph. We next decrease d, and increase the intensity treshold in z-scale (k). We do this until we achieve optimal coverage of emissions. The result is a minimum of ROIs centered on a maximum of maxima. A finetuning centers each ROI weighted by intensity.

LSTM density prediction with imbalance adjusting loss #

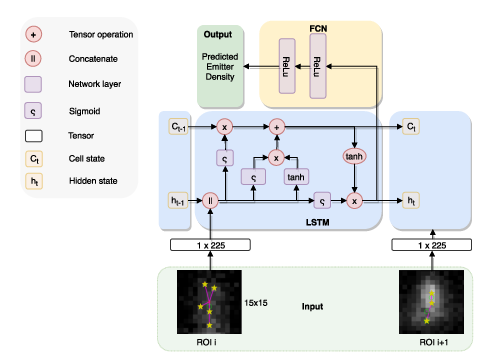
We need to reweight the loss to prevent overfitting to the Poisson \(\lambda\). Returning 1 or 2 for each frame would give up to 85% accuracy, but would fail end user constraints. The problem with reweighting loss functions is that you can cause the majority case to be penalized too much, which is what we don’t want. Instead, if the current loss has a range of [0-1], where 1 is bad, and 0 perfect, then we use the fact that for differentiation it doesn’t matter if we shift the range to [1-2]. This will keep the gradients intact, but will encourage the summation to count the minority cases higher by looking at their inverse frequency, per batch. Let j be the j’th emission to be predicted in a batch of emissions J: $$ W(j) = 2-\frac{f_j} {\Sigma_{j \in J}} $$ We then multiply W(j) with the loss, and continue the training of the LSTM as before. This ensures both the global imbalance, and local (per batch) does not destabilize the loss, while ensuring good unbiased performance of the network.

Results #

Graph tiling is Pareto optimal while compressing stream #

First, we look at the performance of the graph tiling heuristic

We see that it outperforms any fixed threshold approach, and is in fact Pareto optimal. In addition, varying the parameters shows a compression factor of up to 2x can be achieved, which saves compute power needed for the LSTM.

Density prediction using imbalance reweighted LSTM #

The confidence matrices show our approach results in unbiased localization density prediction, evindenced by the results focused on the diagonal.

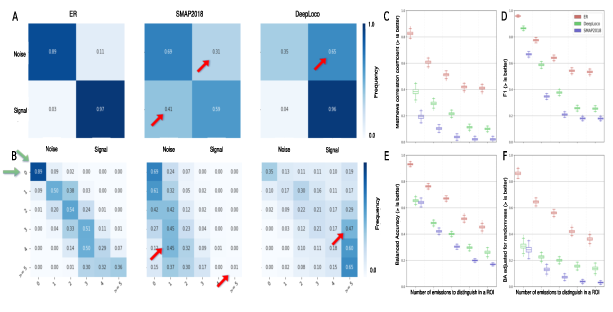
Let’s retake the crossing tubules from the introduction, and now project our (ERGO) predictions, as well as two state of the art approaches.

We color the microtubules by quality of reconstruction, where red indicates overprediction (false positive), white is balanced recovery, and blue is underprediction (false negative). Our results are in the top row, showing a clear balanced result, with competing methods under and over predicting.

Future work #

In future work we’ll apply this to SRM methods that use spectral decomposition for localization, and focus on reconstruction aware localization. In our current work, and most localization algorithms, we do not use the context of what is being localized, but this information can help reconstruct things far better, even subvert information theoretic laws.

For example, if I ask you to fill in the third letter of this word, marked by the question mark, then without any context you have to guess with a uniform probability of 1/26. Or, you could look at the frequency of the last 3rd letter of trigrams to come up with a more accurate prediction, but still, it’s a guessing game.

_ _ ? _ 

However, if I tell you the other letters

H e ? p 

Then with high certainty, if the word is English, ? = a or ? = l. So from 1/26 we now went to 1/2. The same principle can be applied to localizing protein structures in SRM.

Publication #

ERGO was published in IEEE TMI

• Ben Cardoen, Hanene Ben Yedder, Anmol Sharma, Keng C. Chou, Ivan Robert Nabi, and Ghassan Hamarneh. ERGO: Efficient Recurrent Graph Optimized Emitter Density Estimation in Single Molecule Localization Microscopy. IEEE Transactions on Medical Imaging (IEEE TMI), 39(6):1942-1956, http://dx.doi.org/10.1038/s41598-020-77170-3 2020.