A short introduction to Belief Theory: Part 2

In my previous post I introduced (Dempster-Shafer) belief theory, and with it the concepts of encoding evidence into mass, belief and plausibility functions, as well as the concept of conflict of evidence and simple examples that illustrate its utility in evidence based reasoning.

Here we’ll explore the different types of belief functions, and conclude by showing the link with fuzzy computing and possibility theory.

As before, credit goes to the excellent introduction by Yager and Liu: Classic Works of the Dempster-Shafer Theory of Belief Functions: An Introduction.

First, let’s do a quick recap, by way of this illustration:

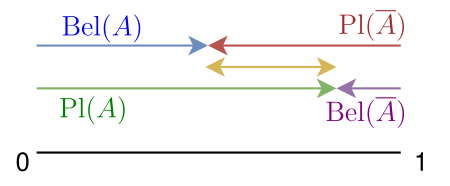
Quick recap #

The problem statement is that we have a question of interest, such as what type of object is in this image?, who committed the crime?, or where are my keys?. We then have a frame of discernment, a term for the set of possible answers or propositions θ. Examples could be The object is a cat, Dave committed murder, or on the countertop, depending on the question.

We have the powerset T = {A | A ⊆ θ}, which is the domain for functions in belief theory. We saw that probability or Bayesian functions are a subset of belief functions, but in general belief functions allow you to express certain concepts, such as ignorance, conflicting evidence, and unknown evidence in a more elegant yet still axiomatic way.

Belief theory assigns each subset A of θ, or element of T a tuple <p, q, r>:

• \(p(A) = Bel(A) \)

• \(q(A) = Pl(A) \)

• \(r(A) = Pl(A)-Bel(A)\)

and we’re given that Pl(A) >= Bel(A).

I’m duplicating the image here so you can spot the <p, q, r> symmetry visually and how they interact with the complement \(\overline{A}\).

The uncertainty r is the difference between the minimum (belief) support and maximum support we have for a (set of) propositions.

Evidence is encoded using mass functions that assing a probabalistic value to focal elements. The terminology may strike you as odd, but they do encode the actual meaning, but please re-read part 1 if you need a refresher. A good heuristic for belief theory is that the terminology makes sense when you understand the concepts, something I wish would be true for many disciplines in science.

Support functions #

While the term belief function is quite general, there are many subtypes, and it is important to know what they are, what their properties are, and when to use which. For example, you may have gotten the impression that I was discarding probabilities or Bayesian belief functions as not that useful, but that would be misreading my attempt at distinguishing the differences between them and general belief functions. If you need the additive property, and you have evidence for each proposition, then by all means, use probabilities. However, if either of the above is false, then you need different functions, so let’s explore which types are out there.

Vacuous belief #

Say you have no evidence, or in other words, a situation of ignorance. Let A ⊂ θ. In belief theory, you’d encode this as:

Evidence:

• \(m(θ) = 1 = Bel(\theta)\)

Belief:

• \(p(A) = Bel(A) = 0 ~~~ \forall A \ne \theta \)

Plausibility:

• \(q(A) = Pl(A) = 1 ~~~ \forall A \ne \emptyset \)

Uncertainty:

• \(r(A) = Pl(A) - Bel(A) = 1 ~~~ \forall A \ne \theta \)

This is a vacuous belief function, because it’s assigning the tuple <0, 1, 1> for any proposition except θ itself, in which case it’s assigning <1, 1, 0>. This matches our intuition, because the only thing this encoding is certain about, is that the answer is in our set of propositions, we just do not have any support for any subset.

In contrast, a probability model would assign <1/n, 1/n, 0> to all elements of θ, with n = | θ |, but this is at best convention, and not related to evidence at all. Due to Bayesian optimization in practice you can never assign exactly 0 or 1 either.

To see why this uniform assumption is not justified in practice, if you’re aksed what the probability is of a coin flip, without any evidence with Bayesian probabilities you have to claim a prior of 1/2. However, this implies a fair coin, yet no evidence for this is present.

Bayesian functions #

In Bayesian functions, we have the following requirements:

• |A| = 1 ∀ ⊂ θ
• Bel(A)=Pl(A)
• Bel(A) is additive

Uncertainty is then 0 for any proposition.

Simple support functions #

Simple support functions fall in between Bayesian and vacuous functions, and are the powerful building blocks of belief theory. Let S ⊂ θ, and let us say we have evidence 0 < s < 1 for 2 focal elements, S and θ.

Evidence:

• \(m(S) = s \)

• \(m(θ) = 1-s \)

• \(m(B) = 0 ~~~ \forall B \notin {S, θ} \)

Belief:

• \(p(θ) = Bel(A) = s ~~~ \forall S \subseteq A \)

• \(p(θ) = Bel(θ) = 1 \)

• \(p(A) =Bel(A) = 0 ~~~ \text{else} \)

Plausibility:

• \(q(A) = Pl(A) = 1 ~~~ \forall A \ne \emptyset \)

Uncertainty:

• \(r(A) = Pl(A) - Bel(A) \)

The link with possibility theory and fuzzy computing #

Simple support functions came into being when Demster generalized Bayesian inference. Dempster then introduced the weight of evidence measure w ∈ [0, +∞). Let m be a simple support function for a focal element S such that m(S) = s and m(θ) = 1-s.

• \(w(s) = -\log(1-s) \)

• \(w(0) = 0 \)

• \(w(1) = +∞ \)

As a sidebar, if you’re not familiar with logarithms, note that 1-s is ∈ [0,1), and thus the log will be negative. Given that the entire range is then negative, we may as well invert the sign, as you’d use negatives only if you also have non-trivial positives. A log transform is a common way of working with probabilities, for example a ratio or difference of probabilities, is computationally very unstable, but transformed this is less often problematic, and log(a/b) = log(a)-log(b).

This means that if you have a general belief function, you could in principle decompose it into separable functions, in that

• \(∃ A, B, \land A\cap B=C\ne ∅ ⇒ ∃ m T→(0,1]: m(A)>0, m(B)>0, m(C)>0 \)

Note that this definition needs a rewrite, I’ll leave to the reader to figure out why. In other words, the non empty intersection of two focal elements is a focal element. This enables separability, will also re-appear later.

Let’s now consider nested focal elements, e.g. let A ⊂ B or B ⊂ A for all A, B ⊂ θ, a separable support function that has such nested focal elements is called a consonant support function.

Why bother? Well, because of the axiomatic definition you now have the following properties:

• \(Bel( A \cup B) = \min(Bel(A), Bel(B)) ~ \forall A, B \subseteq \theta \)

• \(Pl( A \cup B) = \max(Pl(A), Pl(B)) ~ \forall A, B \subseteq \theta \)

The above defines behavior under union of focal elements, but what about intersection?

Let’s also define a consonant support function based on intersection:

• \(f(∅) = 0, f(θ) = 1, f( A \cap B) = \min(f(A), f(B)) ~ \forall A, B \subseteq \theta \)

Great minds think alike, it is often said. Or put differently, human innovation is rarely unique, more likely at a wavefront of similar ideas, or tackling similar problems from refreshingly novel directions.

Zadeh in the 70s proposed, independent of the belief theory framework, possibility and necessity functions, in order to reason in a axiomatic framework about uncertainty, minimum, and maximum support.

And indeed, Zadeh’s possibility is 1-1 with the consonant plausibility function, whereas necessity is 1-1 with the consonant support function.

Apart from the cognitive convergence, if all you care about is practical utility, then the fact that you can know translate advances in either field, and so use the best of either, should be a convincing argument to appreciate the link. In all honesty, the convergence itself, for me, is more valuable than the actual practical advantages, as it speaks to deeper aspects that touch on philosophy of mind, but I’ll keep that to another post.

Conclusion #

We explored the link of belief theory with fuzzy computing, and defined exactly what sources of evidence are encoded how in belief theory so you can start using the theory in practice, in combination with what we discussed in part 1. Next, we will discuss not so obvious but critical shortcomings in what we introduced so far, and how Dempster, Shafer, Zadeh and many many others came up with solutions that are both correct and elegent, my favorite kind.