A short introduction to Belief Theory: Part 1

A subfield of fuzzy computing (FC), Belief Theory, also known as Dempster-Shafer theory, has proven to be quite powerful, yet outside (FC) seems to be less well known, though its concepts are either implicitly or explicitly used in other fields.

This series is an attempt at summarizing the motivations, definitions, axioms, and applications of belief theory.

The material in this post is based in part on the excellent paper Classic works of the Dempster-Shafer theory of belief functions: An introduction by Lipin et al, and could not exist without Dempster’s concept of lower and upper probabilities, and Shafer’s seminal work on evidence theory: A Mathematical Theory of Evidence.

Part 2, which discusses the practical methods of encoding evidence and the link with possibility theory can be found here.

Axiomatic Introduction. #

Suppose you have a question of interest Q, and a set of potential answers θ, or propositions, such that 0 < | θ | < ∞, e.g. θ is finite. θ is also referred to as the frame of discernment. A simple example would be Where are my keys?, then answers could be the set θ = {On the countertop, dropped in sewer grate} where you hope the last one is not true, or at least the probability of the last option is smaller than the rest of the set. We then also define the powerset of θ: \(T = 2^{\theta} = \lbrace A \vert A \subseteq \theta \rbrace \)

A refresher on discrete mathematics will tell you that apart from all real subsets of θ, both θ ∈ T and ∅ ∈ T.

Let’s introduce a family of functions F = {f | f: T → [0,1]} Note that these operate on subsets of θ, not solely elements of θ. You’ll notice that this subtly differs from the family of probability functions P who accept as arguments singleton elements only: \(T’ = \lbrace t ⊂ T | \vert t \vert = 1 \rbrace\), P = {f | f: T → [0,1]} and P ⊂ F. This is an important distinction that will show its value later on.

A real function f : T → [0,1] is a belief function if and only if three axioms hold for f, listed below:

Axiom 1 #

\(f(∅) = 0\)

Intuitively, this reads as: given no answers, the correct one cannot be identified or supported. Belief functions, in contrast to philosophy and religions, are based on quantified evidence and express support for answers.

Axiom 2 #

\(f(θ) = 1\)

One way to read this is: the correct answer is found in the set of all answers.

Axiom 3 #

For subsets Ai ⊂ θ, and 0 < n < +∞ :

\(f(\cup_{i=1}^n A_i) \geq \sum (-1)^{\vert I \vert +1} f(\cap_{i \in I} A_i) ~~~ \text{where} ~~~ I \subset {1,..,n} \land I ≠ ∅\)

Let n=2, and \(A_1 \cap A_2 = ∅\), then axiom 3 will become recognizable, because now it says:

\(f(A_1 \cup A_2) \geq f(A_1) + f(A_2)\)

To keep with notation used by Lipin et al, we’ll refer to belief functions as Bel() rather than f() from now on.

Probability functions on the other hand, would instead of the >= sign have equality, and thus axiom 3 denotes two important observations:

• Probability functions are a subset of belief functions: any probability function is a belief function, but a belief function can express more
• In general, belief functions are not additive, they are not closed under addition on their range, whereas probability functions are
• Belief functions do not require a belief assignment to elements of θ, only to subsets.

Why on earth would we trade in the additive property for a promise of more expressive power, yet to be materialized? Lipin et al illustrate this with two examples, one from Jakob Bernouilli’s Ars Conjectandi.

Elegant ignorance #

First, how do you express ignorance? Ignorance is defined as having a number of potential answers θ, but having no evidence, either probabalistic, or logical, for any of the subsets A ⊂ θ. Using any belief function we can now describe this situation as follows, while keeping the axioms:

• Bel(θ) = 1
• Bel(A) = 0 | A ⊂ θ The first statement says: the answer is enclosed in our set of answers. The second, however, says that we have 0 evidence for any of the potential answers. This belief function is non-additive, there is no way to actually get to the sum of 1 from any subset. Using probability function you would see practitioners state this as:
• Bel(a) = a/|θ| | a ∈ θ But this is a practical workaround to make your probability axioms work, it is not based on any information or evidence at all.

Whodunnit? #

Bernouilli describes another more subtle example. Suppose a man is murdered in a crowd, but there are no witnesses actually observing the murderer. One man, Gracchus, was in the crowd, and when interrogated becomes pale. As you hopefully agree, this nervousness can be due to other reasons than conscience, e.g. fear of being unjustly prosecuted, but even just being cold can induce the same. The evidence is inconclusive: We can’t convict Gracchus on this evidence:

• \(Bel({guilty})<1\)

But even if his pallor is due to other reasons, that does not mean he is innocent either

• \(Bel({innocent})=0\)

Yet Bel(θ)=1, and so this belief function is not additive. If we were to model this with a probability function, you’d be forced to either assume ‘innocent until proven guilty’, or 50/50 odds, neither of which are supported by the actual evidence, so your choice of function is not as expressive as it could be.

The perfect quote that captures this distinction, is by Daniel J. Boorstin:

The greatest enemy of knowledge is not ignorance, but the illusion of knowledge

Freedom in dividing belief #

Earlier we mentioned that belief functions work on subsets, and do not require your assign belief values on individual elements, unless you actually want to. The deepest level of division, e.g. those smallest subsets of θ that do have an assignment, are called focal elements, which have a probability number assignment function m which respects the following axiom:

• \(\sum_{A \subseteq \theta} m(A)=1 \)

With the added implication that there is no assignment m(A) for any A’ ⊂ A, ∀ A ⊂ θ.

With m given, you can now express belief functions:

• \(Bel(A) = \sum_{m(B) \subseteq A} m(B) \)

Suppose you have A={a, b}, this then states simply that:

• \(Bel(A) = m(∅)+m({a})+m({b})+m(A), \)

and so we need to add the boundary condition m(∅)=0.

You can invert the relation between belief and mass m by a recursive deduction:

• \(m(∅)=0\)

• \(m(A) = Bel(A) - \sum_{B ⊂ A} m(B), \)

For completeness, Liu and Yager show an equivalent with a Möbius transformation, but I’m not familiar with the underlying transform and I find the recursive version very elegant. Note how it illustrates the topdown division of belief up until the assignment of focal elements.

Negation and divisibility #

The belief in A is not directly related to the belief in the negation of A, noted as \(\overline A \), because of the limited divisibility. However, Bel(A) does change the likelihood, credibility, or plausibility of \(\overline A \). Let us then capture this in a formal plausibility function:

• \(Pl(A) = 1 - Bel(\overline A) = \sum_{A \cap B \neq ∅} m(B)\)

In other words \(\overline A \) expresses the negation of subset of answers A. If you have a Belief in \(\overline A \), say 0.3, then the plausibility of A must be 0.7. What about its belief then? You can show that the plausibility of a proposition is equal or greater than the belief in the proposition:

• \(Pl(A) >= Bel(A)\)

And here we have the link with lower and upper probabilities, the belief is the minimum assignment to a proposition, whereas the plausibility coincides with the maximum, based on what you collected as mass functions (probabalistic evidence) and logical derivation.

Linking evidence, belief, and plausibility. #

So far you may have assumed there is only 1 mass function assignment, but this is not true. In fact, the link with evidence are your mass functions.

Say you have 2 pieces of evidence, that give credence to some of the answers (θ). Note how this plain English translates ‘some of’ as subsets. This is then expressed as \(m_1, m_2\). Combining evidence is then done by the Dempster’s combination rule:

• \(m(A) = \frac{\sum_{B \cap C = A} m_1(B)m_2(C)}{\sum_{B \cap C \neq ∅} m_1(B)m_2(C)}\)

The denominator indicates conflict, leading to the formulation of weight of conflict:

• \(W = \log \frac{1}{\sum_{B \cap C \neq ∅} m_1(B)m_2(C)} = -\log(\sum_{B \cap C \neq ∅} m_1(B)m_2(C))\)

and this also allows you to define when any two mass functions, or pieces of evidence, can be combined, because W has to be finite.

The bankrobber example #

To illustrate the expressive power of this system of reasoning, the authors come up with a bank robbery, and three suspects: A, B, C. Our question of interest is “Who committed the crime?” and the frame of discernment θ = {A, B, C}. The evidence is, as it is in real life, complex and incomplete. First we’re told that there is a not so great camera that in grainy pixels allows detectives to conclude that it’s 4x more likely for the suspect, caught in a fleeting glimpse, to have green eyes versus brown. We’re told that B has green eyes, so

• \(m_1({B})=0.8, m_1({A, C})=0.2\)

Next, we have a witness with poor eyesight, whose credibility is at 60%, and identifies in a line up A and C.

• \(m_2({A, C})=0.6, m_2({A, B, C})=0.4\)

Note how the second evidence is not symmetric, because if the witness is not believable or credible, the alternative is inconclusive. In the first evidence function it’s an exclusive, where you have a ratio of probabilities that exclude.

First, we have 2 focal elements: {A, C} and {B}, there is no other finer assignment.

Using Dempster’s rule we can now combine these, the weight of conflict is

• \(\log(\frac{1}{1-0.48})\)

This follows from \(m_1({A,C}) * m2({B})\) which has an empty intersection, and 0.8*0.6 = 0.48.

We end up with \(m({B})=\frac{ 0.8 * 0.4}{1-0.8 * 0.6} = 0.615\) and \(m({A,C})=\frac{ 0.6 * 0.2 + 0.2 * 0.8 }{1-0.8 * 0.6} = 0.385\) for the combined evidence.

We can conclude B is the more likely suspect, by roughly a factor of 2.

Conclusion #

In a subsequent post I’ll delve into the finer details of conflict, support functions, and some applications to illustrate more of the theory, but what we covered so far should give you a gentle introduction.

I hope you’ll appreciate the nuanced elegance of belief theory, and to underline this I’ll finish with an illustration of the plausibility and belief functions as dual functions.

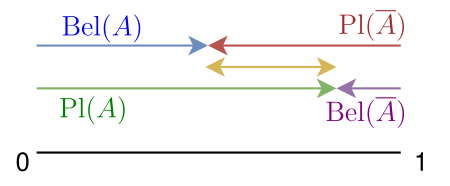
Note the orange arrow? That is the concept of uncertainty, the exact distance between the minimum support you have for proposition A, the belief, and the maximum support, the plausibility.

Credit goes to the excellent introduction by Yager and Liu: Classic Works of the Dempster-Shafer Theory of Belief Functions: An Introduction.